Research Assistant | M.Sc. Computer Sience
+49 30 314 73104
MAR 6.037
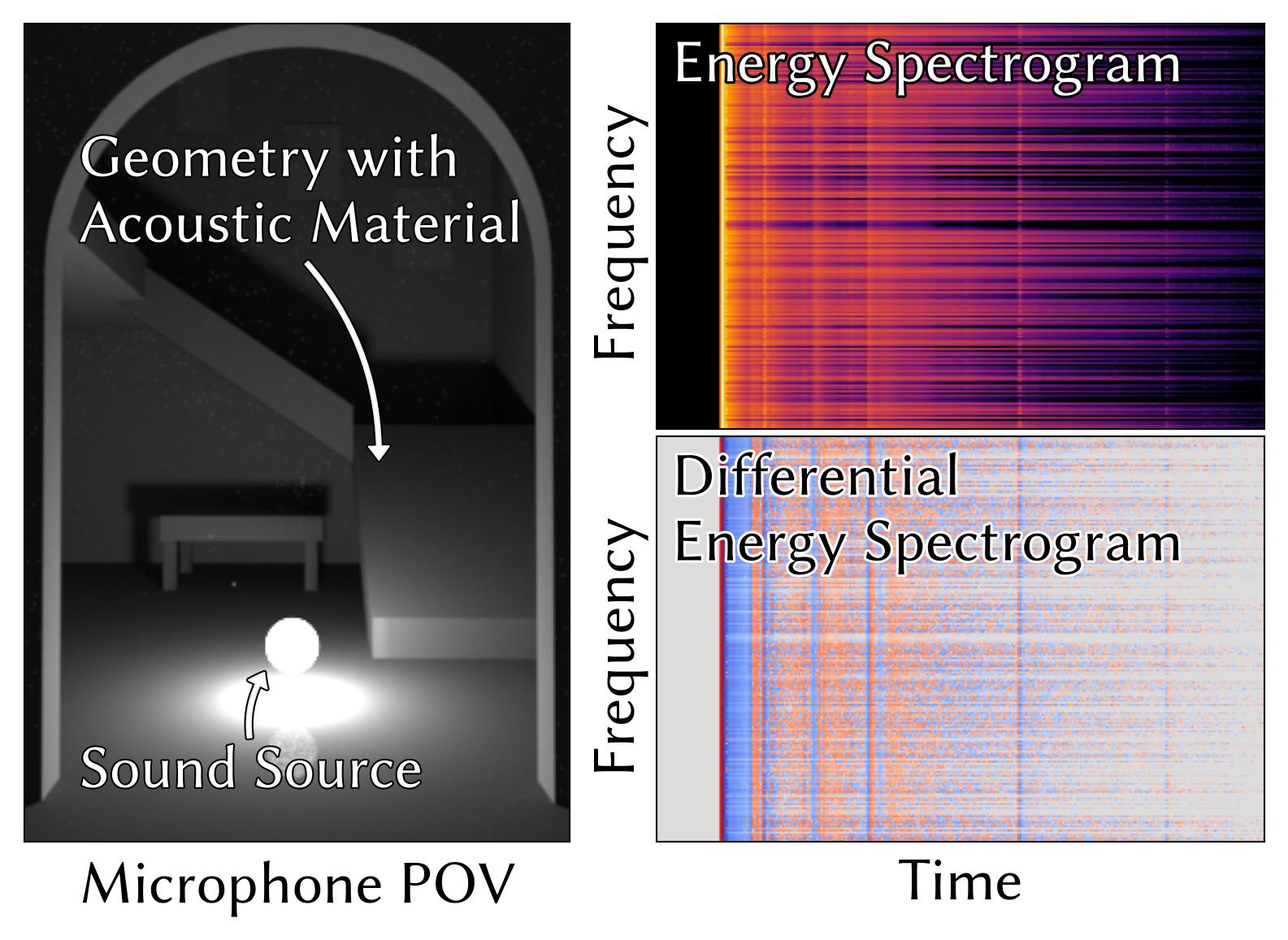 Differentiable Geometric Acoustic Path Tracing using Time-Resolved Path Replay Backpropagation (2025)
ACM Transactions on Graphics (Proc. of SIGGRAPH)
Differentiable Geometric Acoustic Path Tracing using Time-Resolved Path Replay Backpropagation (2025)
ACM Transactions on Graphics (Proc. of SIGGRAPH)
@article{finnendahl:2025:diffacousticpt,
author = {Finnendahl, Ugo and Worchel, Markus and J\"{u}terbock, Tobias and Wujecki, Daniel and Brinkmann, Fabian and Weinzierl, Stefan and Alexa, Marc},
title = {Differentiable Geometric Acoustic Path Tracing using Time-Resolved Path Replay Backpropagation},
year = {2025},
issue_date = {August 2025},
publisher = {Association for Computing Machinery},
address = {New York, NY, USA},
volume = {44},
number = {4},
issn = {0730-0301},
url = {https://doi.org/10.1145/3730900},
doi = {10.1145/3730900},
journal = {ACM Trans. Graph.},
month = jul,
articleno = {82},
numpages = {17},
keywords = {differentiable rendering, geometrical acoustics, physically-based simulation, acoustic optimization}
}
 Radiative Backpropagation with Non-Static Geometry (2025)
Eurographics Symposium on Rendering (EGSR)
Radiative Backpropagation with Non-Static Geometry (2025)
Eurographics Symposium on Rendering (EGSR)
@inproceedings{10.2312:sr.20251198,
booktitle = {Eurographics Symposium on Rendering},
editor = {Wang, Beibei and Wilkie, Alexander},
title = {{Radiative Backpropagation with Non-Static Geometry}},
author = {Worchel, Markus and Finnendahl, Ugo and Alexa, Marc},
year = {2025},
publisher = {The Eurographics Association},
ISSN = {1727-3463},
ISBN = {978-3-03868-292-9},
DOI = {10.2312/sr.20251198}
}
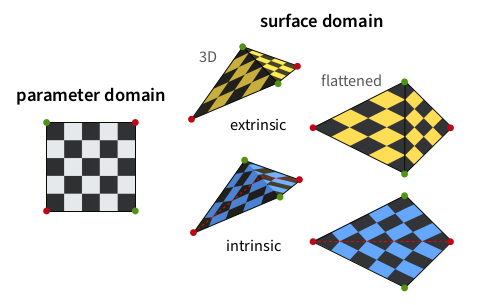 Mesh Parameterization meets Intrinsic Triangulations (2024)
Computer Graphics Forum
Mesh Parameterization meets Intrinsic Triangulations (2024)
Computer Graphics Forum
@article{Akalin:2024:MPIT,
author = {Akalin, Koray and Finnendahl, Ugo and Sorkine-Hornung, Olga and Alexa, Marc},
title = {Mesh Parameterization Meets Intrinsic Triangulations},
journal = {Computer Graphics Forum},
volume = {43},
number = {5},
pages = {e15134},
keywords = {CCS Concepts, ⢠Computing methodologies â Computer graphics, Mesh models, Mesh geometry models},
doi = {https://doi.org/10.1111/cgf.15134},
url = {https://onlinelibrary.wiley.com/doi/abs/10.1111/cgf.15134},
eprint = {https://onlinelibrary.wiley.com/doi/pdf/10.1111/cgf.15134},
abstract = {A parameterization of a triangle mesh is a realization in the plane so that all triangles have positive signed area. Triangle mesh parameterizations are commonly computed by minimizing a distortion energy, measuring the distortions of the triangles as they are mapped into the parameter domain. It is assumed that the triangulation is fixed and the triangles are mapped affinely. We consider a more general setup and additionally optimize among the intrinsic triangulations of the piecewise linear input geometry. This means the distortion energy is computed for the same geometry, yet the space of possible parameterizations is enlarged. For minimizing the distortion energy, we suggest alternating between varying the parameter locations of the vertices and intrinsic flipping. We show that this process improves the mapping for different distortion energies at moderate additional cost. We also find intrinsic triangulations that are better starting points for the optimization of positions, offering a compromise between the full optimization approach and exploiting the additional freedom of intrinsic triangulations.},
year = {2024}
}
 Fitting Flats to Flats (2024)
Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR)
Fitting Flats to Flats (2024)
Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR)
@InProceedings{Dogadov:2024:Flats,
author = {Dogadov, Gabriel and Finnendahl, Ugo and Alexa, Marc},
title = {Fitting Flats to Flats},
booktitle = {Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR)},
month = {June},
year = {2024}
}
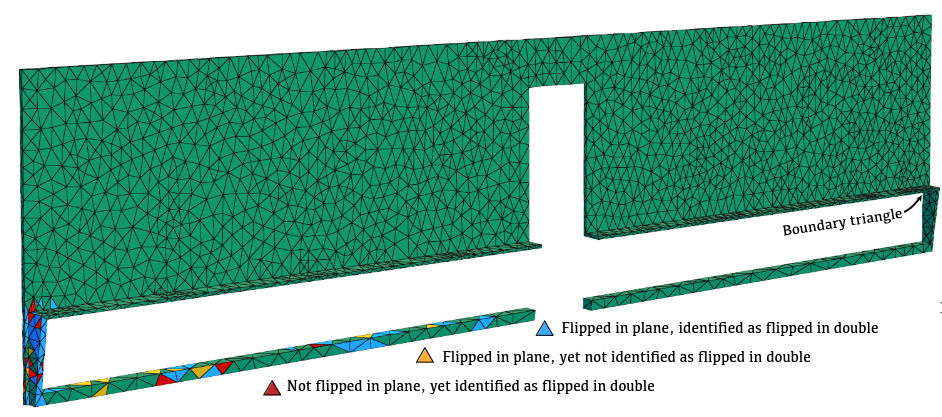 Efficient Embeddings in Exact Arithmetic (2023)
ACM Transactions on Graphics
Efficient Embeddings in Exact Arithmetic (2023)
ACM Transactions on Graphics
@article{10.1145/3592445,
author = {Finnendahl, Ugo and Bogiokas, Dimitrios and Robles Cervantes, Pablo and Alexa, Marc},
title = {Efficient Embeddings in Exact Arithmetic},
year = {2023},
issue_date = {August 2023},
publisher = {Association for Computing Machinery},
address = {New York, NY, USA},
volume = {42},
number = {4},
issn = {0730-0301},
url = {https://doi.org/10.1145/3592445},
doi = {10.1145/3592445},
abstract = {We provide a set of tools for generating planar embeddings of triangulated topological spheres. The algorithms make use of Schnyder labelings and realizers. A new representation of the realizer based on dual trees leads to a simple linear time algorithm mapping from weights per triangle to barycentric coordinates and, more importantly, also in the reverse direction. The algorithms can be implemented so that all coefficients involved are 1 or -1. This enables integer computation, making all computations exact. Being a Schnyder realizer, mapping from positive triangle weights guarantees that the barycentric coordinates form an embedding. The reverse direction enables an algorithm for fixing flipped triangles in planar realizations, by mapping from coordinates to weights and adjusting the weights (without forcing them to be positive). In a range of experiments, we demonstrate that all algorithms are orders of magnitude faster than existing robust approaches.},
journal = {ACM Trans. Graph.},
month = {jul},
articleno = {71},
numpages = {17},
keywords = {integer coordinates, parametrization, schnyder labeling}
}
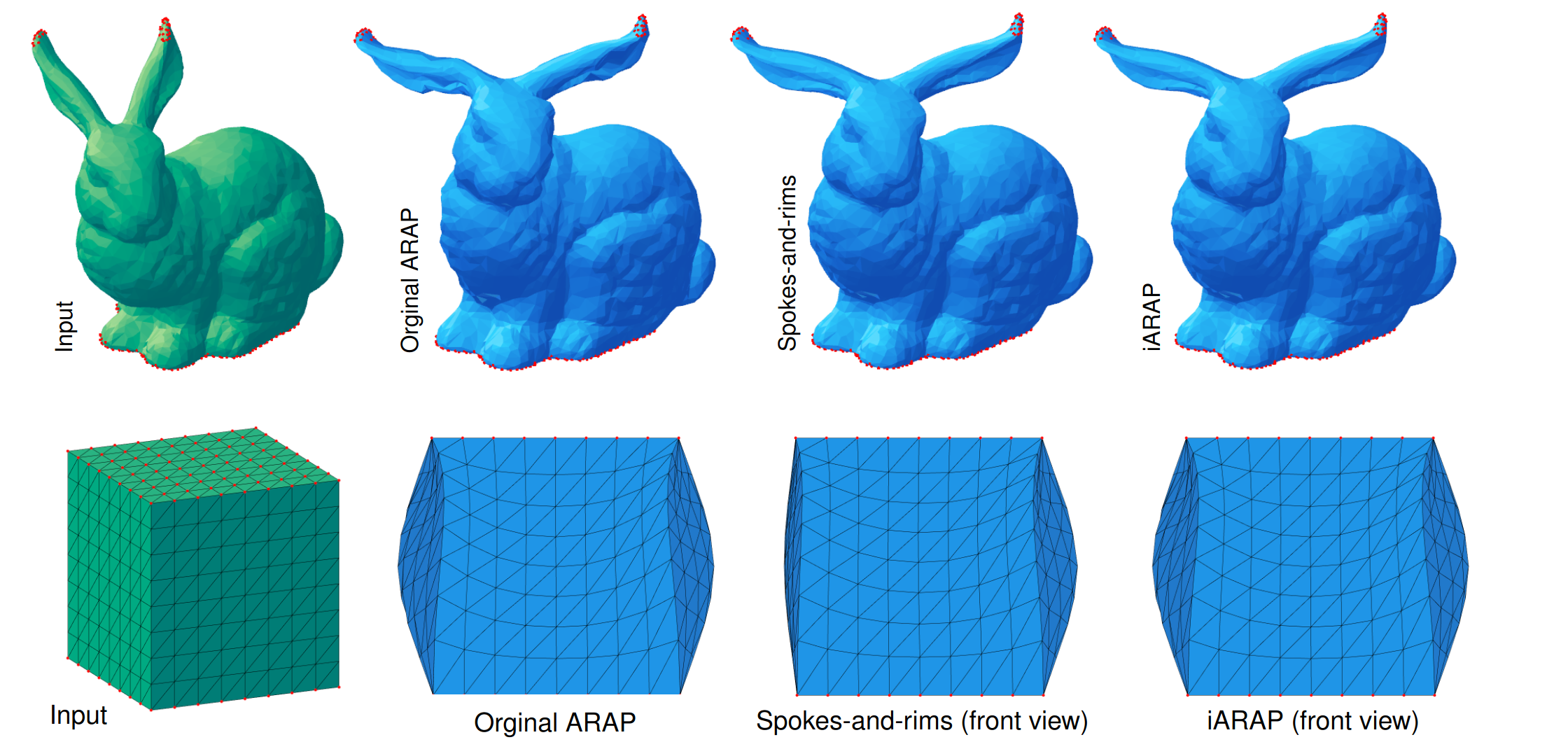 ARAP Revisited: Discretizing the Elastic Energy using Intrinsic Voronoi Cells (2023)
Computer Graphics Forum
ARAP Revisited: Discretizing the Elastic Energy using Intrinsic Voronoi Cells (2023)
Computer Graphics Forum
@article{Finnendahl:2023:AR,
author = {Finnendahl, Ugo and Schwartz, Matthias and Alexa, Marc},
title = {ARAP Revisited: Discretizing the Elastic Energy using Intrinsic Voronoi Cells},
journal = {Computer Graphics Forum},
year={2023},
volume = {43},
number = {5},
pages = {e15134},
keywords = {modelling, deformations, polygonal modelling},
doi = {https://doi.org/10.1111/cgf.14790},
url = {https://onlinelibrary.wiley.com/doi/abs/10.1111/cgf.14790},
eprint = {https://onlinelibrary.wiley.com/doi/pdf/10.1111/cgf.14790},
abstract = {Abstract As-rigid-as-possible (ARAP) surface modelling is widely used for interactive deformation of triangle meshes. We show that ARAP can be interpreted as minimizing a discretization of an elastic energy based on non-conforming elements defined over dual orthogonal cells of the mesh. Using the intrinsic Voronoi cells rather than an orthogonal dual of the extrinsic mesh guarantees that the energy is non-negative over each cell. We represent the intrinsic Delaunay edges extrinsically as polylines over the mesh, encoded in barycentric coordinates relative to the mesh vertices. This modification of the original ARAP energy, which we term iARAP, remedies problems stemming from non-Delaunay edges in the original approach. Unlike the spokes-and-rims version of the ARAP approach it is less susceptible to the triangulation of the surface. We provide examples of deformations generated with iARAP and contrast them with other versions of ARAP. We also discuss the properties of the Laplace-Beltrami operator implicitly introduced with the new discretization.}
}
 Gauss Stylization: Interactive Artistic Mesh Modeling based on Preferred Surface Normals (2021)
Computer Graphics Forum
Gauss Stylization: Interactive Artistic Mesh Modeling based on Preferred Surface Normals (2021)
Computer Graphics Forum
@article{Kohlbrenner2021,
title = {Gauss Stylization: Interactive Artistic Mesh Modeling based on Preferred Surface Normals},
author = {Max Kohlbrenner and Ugo Finnendahl and Tobias Djuren and Marc Alexa},
url = {https://cybertron.cg.tu-berlin.de/projects/gaussStylization/},
doi = {https://doi.org/10.1111/cgf.14355},
year = {2021},
date = {2021-08-23},
journal = {Computer Graphics Forum},
volume = {40},
number = {5},
pages = {33-43},
abstract = {Abstract Extending the ARAP energy with a term that depends on the face normal, energy minimization becomes an effective stylization tool for shapes represented as meshes. Our approach generalizes the possibilities of Cubic Stylization: the set of preferred normals can be chosen arbitrarily from the Gauss sphere, including semi-discrete sets to model preference for cylinder- or cone-like shapes. The optimization is designed to retain, similar to ARAP, the constant linear system in the global optimization. This leads to convergence behavior that enables interactive control over the parameters of the optimization. We provide various examples demonstrating the simplicity and versatility of the approach.},
keywords = {computer graphics, geometric stylization, geometry processing, non-photorealistic rendering, shape modeling},
pubstate = {published},
tppubtype = {article}
}