Research Assistant | M.Sc. Computer Science
MAR 6.039
 Interpolating splines over triangulated surfaces by blending vertex-centric local geometries (2025)
Computers & Graphics
Interpolating splines over triangulated surfaces by blending vertex-centric local geometries (2025)
Computers & Graphics
@article{DJUREN2025104316,
title = {Interpolating splines over triangulated surfaces by blending vertex-centric local geometries},
journal = {Computers & Graphics},
volume = {131},
pages = {104316},
year = {2025},
issn = {0097-8493},
doi = {https://doi.org/10.1016/j.cag.2025.104316},
url = {https://www.sciencedirect.com/science/article/pii/S0097849325001578},
author = {Tobias Djuren and Ugo Finnendahl and Maximilian Kohlbrenner and Markus Worchel and Marc Alexa},
keywords = {Rational interpolation, Splines, Local control},
abstract = {We investigate the construction of visually smooth spline surfaces that interpolate the vertices of triangulations by blending local patches. Each triangle star carries a locally interpolating surface patch. The patches are only required to interpolate the vertex, whereas in previous methods the patches are often defined per edge, imposing multiple constraints on local approximations. We adopt simple rational blend functions for the triangular domains, that are constructed so that they retain the interpolation and tangent behavior on the patch boundaries. Decoupling local approximation from blending facilitates the exploration of visually pleasing constructions, while controlling the complexity.}
}
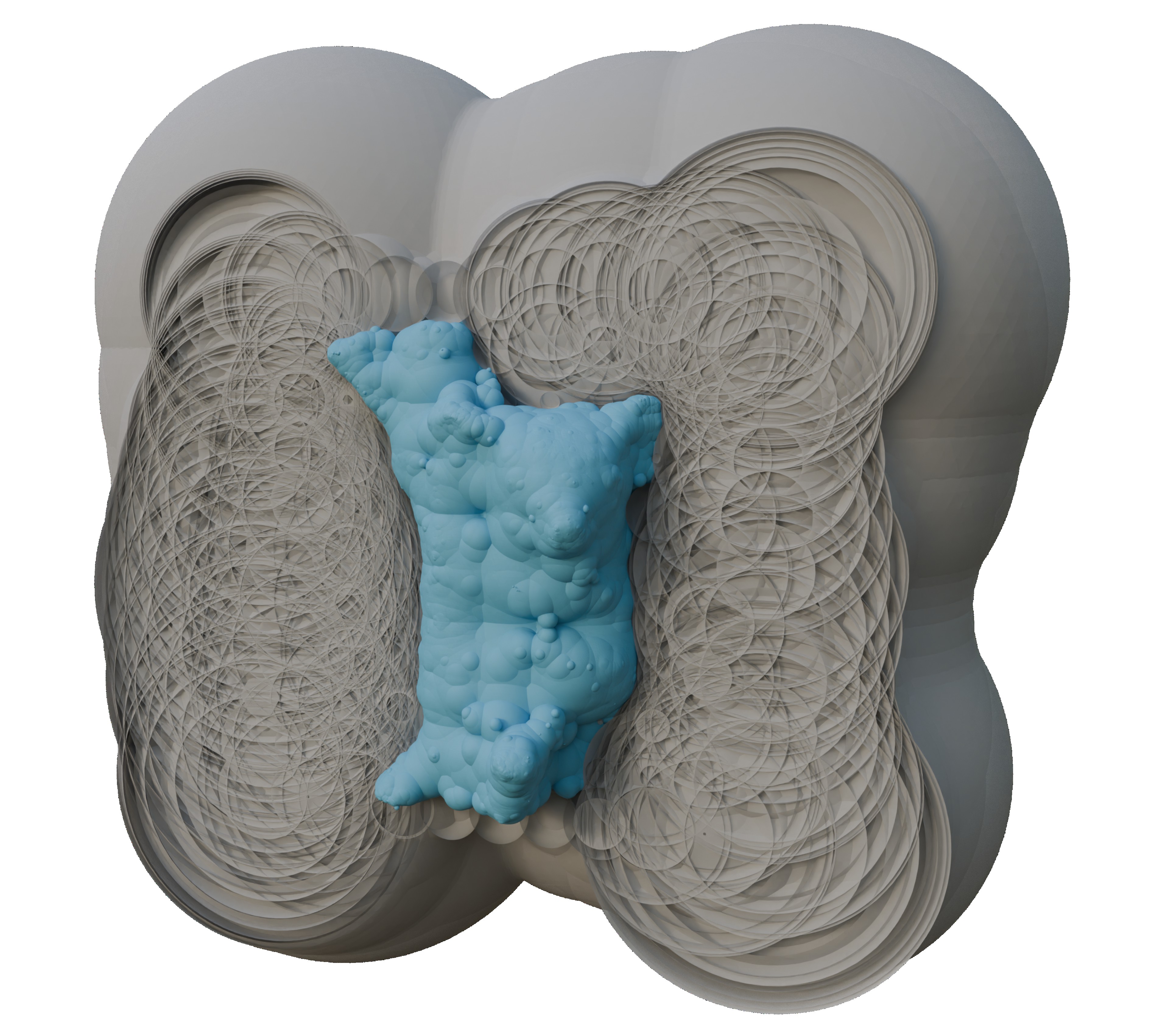 A Polyhedral Construction of Empty Spheres in Discrete Distance Fields (2025)
ACM SIGGRAPH 2025 Conference Proceedings
A Polyhedral Construction of Empty Spheres in Discrete Distance Fields (2025)
ACM SIGGRAPH 2025 Conference Proceedings
@inproceedings{10.1145/3721238.3730748,
author = {Kohlbrenner, Maximilian and Alexa, Marc},
title = {A Polyhedral Construction of Empty Spheres in Discrete Distance Fields},
year = {2025},
isbn = {9798400715402},
publisher = {Association for Computing Machinery},
address = {New York, NY, USA},
url = {https://doi.org/10.1145/3721238.3730748},
doi = {10.1145/3721238.3730748},
abstract = {Lie sphere geometry provides a unified representation of points, oriented spheres and hyperplanes in Euclidean d-space as the subset of lines in ( mathbb {R}^{d+3} ) that are contained in a certain quadric. The natural scalar product in this construction is zero if two elements are in oriented contact. We show how the sign of this product can be used to decide if spheres are disjoint. This allows us to model the space of spheres that are not intersecting a given union of spheres as the intersection of half-spaces (and the quadric). The maximal spheres are on the boundary of this set and can be computed by first constructing the intersection of half-spaces, which is a convex hull problem, and then intersecting edges of the hull against the quadric, which are the roots of a univariate quadratic. We demonstrate the method at the example of contouring a discrete signed distance field: every sample of the signed distance field represents an empty spheres and the zero-level contour has to be disjoint from the union of these spheres. Maximal spheres outside the empty spheres provide samples on the zero-level contour. The quality of this sample set is comparable to existing methods relying on optimization, while being deterministic and faster in practice.},
booktitle = {Proceedings of the Special Interest Group on Computer Graphics and Interactive Techniques Conference Conference Papers},
articleno = {22},
numpages = {10},
keywords = {Lie sphere geometry, polyhedra, discrete distance fields, maximal empty spheres},
location = {
},
series = {SIGGRAPH Conference Papers '25}
}
 Symmetrized Poisson Reconstruction (2025)
Computer Graphics Forum
Symmetrized Poisson Reconstruction (2025)
Computer Graphics Forum
@article{10.1111:cgf.70210
,
journal = {Computer Graphics Forum},
title = {{Symmetrized Poisson Reconstruction
}},
author = {Kohlbrenner, Maximilian and
Liu, Hongyi and
Alexa, Marc and
Kazhdan, Misha
},
year = {2025
},
publisher = {The Eurographics Association and John Wiley & Sons Ltd.
},
ISSN = {1467-8659
},
DOI = {10.1111/cgf.70210
}
}
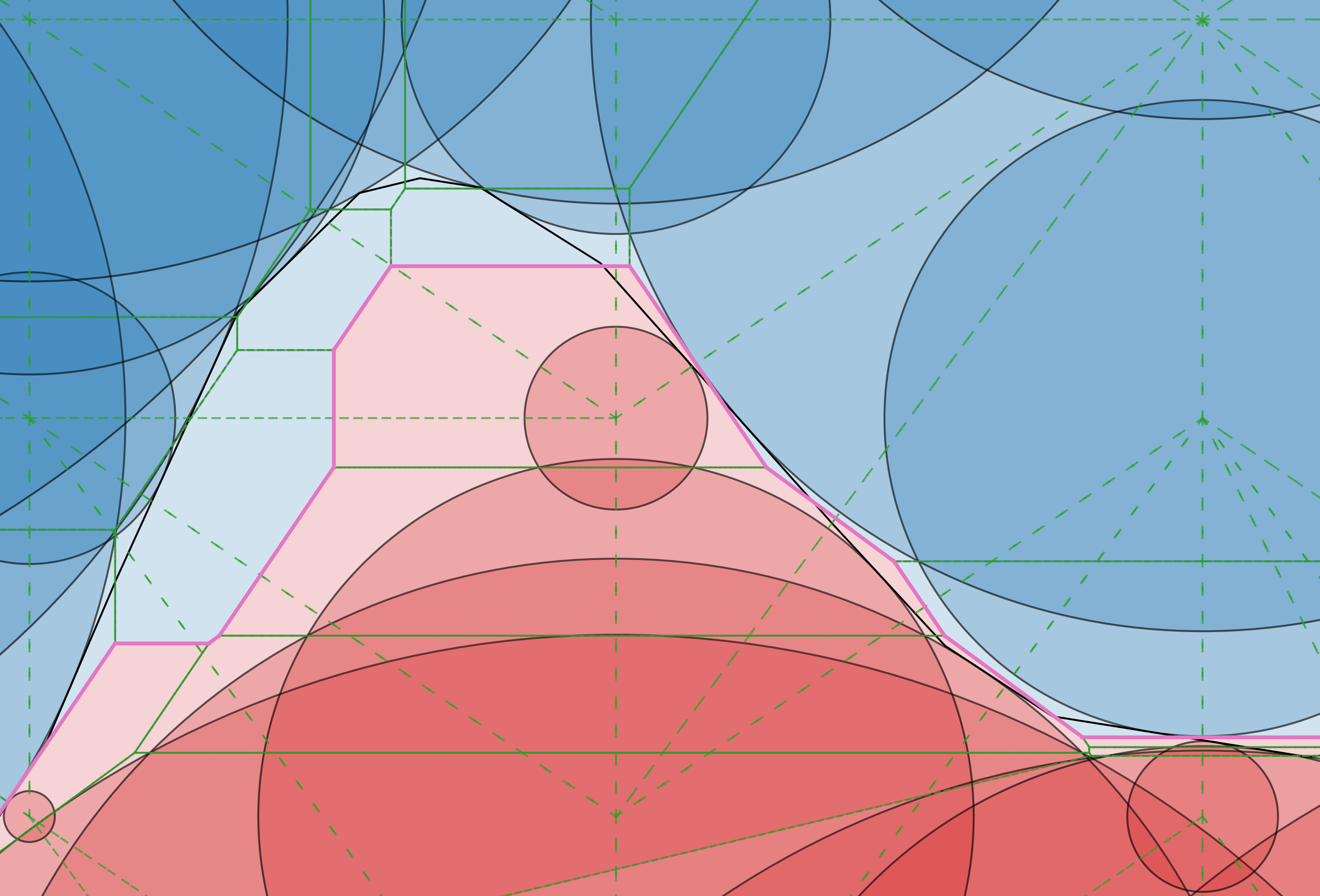 Isosurface Extraction for Signed Distance Functions using Power Diagrams (2025)
Eurographics 2025
Isosurface Extraction for Signed Distance Functions using Power Diagrams (2025)
Eurographics 2025
 K-Surfaces: Bézier-Splines Interpolating at Gaussian Curvature Extrema (2023)
ACM Transactions on Graphics (Proc. of SIGGRAPH Asia)
K-Surfaces: Bézier-Splines Interpolating at Gaussian Curvature Extrema (2023)
ACM Transactions on Graphics (Proc. of SIGGRAPH Asia)
@article{10.1145/3618383,
author = {Djuren, Tobias and Kohlbrenner, Maximilian and Alexa, Marc},
title = {K-Surfaces: B\'{e}zier-Splines Interpolating at Gaussian Curvature Extrema},
year = {2023},
issue_date = {December 2023},
publisher = {Association for Computing Machinery},
address = {New York, NY, USA},
volume = {42},
number = {6},
issn = {0730-0301},
url = {https://doi.org/10.1145/3618383},
doi = {10.1145/3618383},
journal = {ACM Trans. Graph.},
month = {dec},
articleno = {210},
numpages = {13},
keywords = {interactive surface modeling, b\'{e}zier patches, gaussian curvature, b\'{e}zier splines}
}
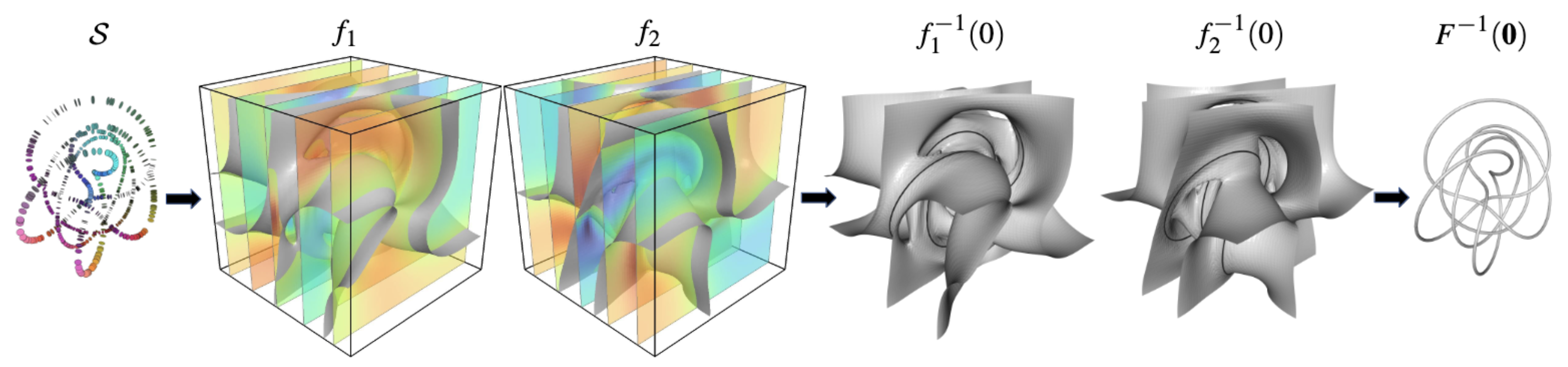 Poisson Manifold Reconstruction — Beyond Co-dimension One (2023)
Computer Graphics Forum
Poisson Manifold Reconstruction — Beyond Co-dimension One (2023)
Computer Graphics Forum
@article{https://doi.org/10.1111/cgf.14907,
author = {Kohlbrenner, M. and Lee, S. and Alexa, M. and Kazhdan, M.},
title = {Poisson Manifold Reconstruction — Beyond Co-dimension One},
journal = {Computer Graphics Forum},
volume = {42},
number = {5},
pages = {e14907},
keywords = {CCS Concepts, • Computing methodologies → Shape modeling, • Mathematics of computing → Nonlinear equations, Numerical analysis, curve and surface reconstruction, sub-manifold reconstruction, exterior product, polynomial optimization},
doi = {https://doi.org/10.1111/cgf.14907},
url = {https://onlinelibrary.wiley.com/doi/abs/10.1111/cgf.14907},
eprint = {https://onlinelibrary.wiley.com/doi/pdf/10.1111/cgf.14907},
abstract = {Abstract Screened Poisson Surface Reconstruction creates 2D surfaces from sets of oriented points in 3D (and can be extended to co-dimension one surfaces in arbitrary dimensions). In this work we generalize the technique to manifolds of co-dimension larger than one. The reconstruction problem consists of finding a vector-valued function whose zero set approximates the input points. We argue that the right extension of screened Poisson Surface Reconstruction is based on exterior products: the orientation of the point samples is encoded as the exterior product of the local normal frame. The goal is to find a set of scalar functions such that the exterior product of their gradients matches the exterior products prescribed by the input points. We show that this setup reduces to the standard formulation for co-dimension 1, and leads to more challenging multi-quadratic optimization problems in higher co-dimension. We explicitly treat the case of co-dimension 2, i.e., curves in 3D and 2D surfaces in 4D. We show that the resulting bi-quadratic problem can be relaxed to a set of quadratic problems in two variables and that the solution can be made effective and efficient by leveraging a hierarchical approach.},
year = {2023}
}
 Gauss Stylization: Interactive Artistic Mesh Modeling based on Preferred Surface Normals (2021)
Computer Graphics Forum
Gauss Stylization: Interactive Artistic Mesh Modeling based on Preferred Surface Normals (2021)
Computer Graphics Forum
@article{Kohlbrenner2021,
title = {Gauss Stylization: Interactive Artistic Mesh Modeling based on Preferred Surface Normals},
author = {Max Kohlbrenner and Ugo Finnendahl and Tobias Djuren and Marc Alexa},
url = {https://cybertron.cg.tu-berlin.de/projects/gaussStylization/},
doi = {https://doi.org/10.1111/cgf.14355},
year = {2021},
date = {2021-08-23},
journal = {Computer Graphics Forum},
volume = {40},
number = {5},
pages = {33-43},
abstract = {Abstract Extending the ARAP energy with a term that depends on the face normal, energy minimization becomes an effective stylization tool for shapes represented as meshes. Our approach generalizes the possibilities of Cubic Stylization: the set of preferred normals can be chosen arbitrarily from the Gauss sphere, including semi-discrete sets to model preference for cylinder- or cone-like shapes. The optimization is designed to retain, similar to ARAP, the constant linear system in the global optimization. This leads to convergence behavior that enables interactive control over the parameters of the optimization. We provide various examples demonstrating the simplicity and versatility of the approach.},
keywords = {computer graphics, geometric stylization, geometry processing, non-photorealistic rendering, shape modeling},
pubstate = {published},
tppubtype = {article}
}
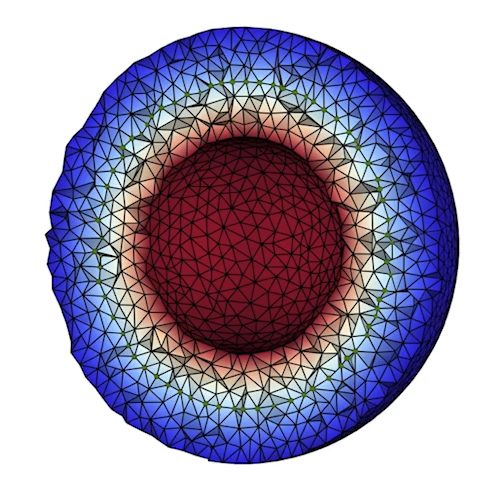 Properties of Laplace Operators for Tetrahedral Meshes (2020)
Computer Graphics Forum
Properties of Laplace Operators for Tetrahedral Meshes (2020)
Computer Graphics Forum
@article{Alexa:2020:PLO,
title = {Properties of Laplace Operators for Tetrahedral Meshes},
author = {Marc Alexa and Philipp Herholz and Maximilian Kohlbrenner and Olga Sorkine},
url = {https://igl.ethz.ch/projects/LB3D/, Project Page},
doi = {10.1111/cgf.14068},
year = {2020},
date = {2020-07-06},
journal = {Computer Graphics Forum},
volume = {39},
number = {5},
pages = {55-68},
abstract = {Discrete Laplacians for triangle meshes are a fundamental tool in geometry processing. The so-called cotan Laplacian is widely used since it preserves several important properties of its smooth counterpart. It can be derived from different principles: either considering the piecewise linear nature of the primal elements or associating values to the dual vertices. Both approaches lead to the same operator in the two-dimensional setting. In contrast, for tetrahedral meshes, only the primal construction is reminiscent of the cotan weights, involving dihedral angles. We provide explicit formulas for the lesser-known dual construction. In both cases, the weights can be computed by adding the contributions of individual tetrahedra to an edge. The resulting two different discrete Laplacians for tetrahedral meshes only retain some of the properties of their two-dimensional counterpart. In particular, while both constructions have linear precision, only the primal construction is positive semi-definite and only the dual construction generates positive weights and provides a maximum principle for Delaunay meshes. We perform a range of numerical experiments that highlight the benefits and limitations of the two constructions for different problems and meshes.},
keywords = {computer graphics, geometry processing, laplacian},
pubstate = {published},
tppubtype = {article}
}